Gauss Law for electric fields is a fundamental principle in electromagnetism, one of Maxwell’s four equations. It provides a powerful way to relate the distribution of electric charge to the electric field it produces.
Statement of Gauss’s Law:
Gauss’s law for electricity states that the total electric flux (Φ) through any closed surface (also called a Gaussian surface) is directly proportional to the net electric charge (Qenc) enclosed by that surface.

Mathematical Formula:
The law is expressed mathematically as:
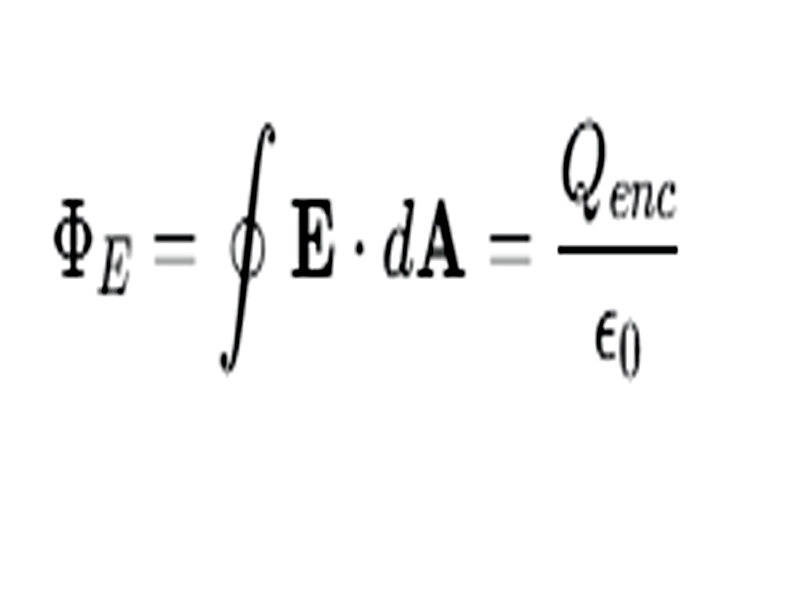
Where:
- ΦE is the electric flux through the closed surface.
- E is the electric field vector.
- dA is a differential area vector, with its magnitude equal to the area of the differential surface element and its direction perpendicular to the surface, pointing outward.
- ∮ indicates an integral over a closed surface.
- Qenc is the total net electric charge enclosed within the Gaussian surface.
- ϵ0 is the permittivity of free space, a fundamental physical constant with an approximate value of 8.854×10−12 C2/(N⋅m2).
Key Concepts:
- Electric Flux: Electric flux is a measure of the “flow” of the electric field through a surface. It’s proportional to the number of electric field lines passing through the surface. A positive flux indicates more field lines leaving the surface than entering, while a negative flux indicates more field lines entering. If no charges are enclosed, the net flux is zero (meaning the number of field lines entering equals the number leaving).
- Gaussian Surface: This is an imaginary closed surface chosen to simplify the calculation of the electric field. The key to using Gauss’s Law effectively is to choose a Gaussian surface that takes advantage of the symmetry of the charge distribution.
- Charge Enclosure: The total charge Qenc inside the Gaussian surface determines the total flux. If there is no charge enclosed, the flux will be zero.
- Symmetry: Gauss’s law is most useful when there is symmetry in the problem (e.g., spherical, cylindrical, or planar symmetry), because it allows us to calculate the electric field directly without needing to know the exact configuration of the charge distribution.
Example: Electric Field of a Point Charge
For a point charge Q at the center of a spherical Gaussian surface of radius r, Gauss’s law simplifies to:

This is Coulomb’s law, which gives the electric field due to a point charge.
Applications of Gauss’s Law:
While Gauss’s Law is always true for any closed surface, it is particularly useful for calculating electric fields in situations with high symmetry. By choosing an appropriate Gaussian surface, the integral can often be simplified significantly, allowing for straightforward calculation of the electric field. Common applications include finding the electric field due to:
- A point charge: By choosing a spherical Gaussian surface centered on the charge.
- A uniformly charged infinite line: By choosing a cylindrical Gaussian surface coaxial with the line.
- A uniformly charged infinite plane sheet: By choosing a cylindrical or rectangular Gaussian surface with its axis perpendicular to the plane.
- A uniformly charged spherical shell or solid sphere: By choosing spherical Gaussian surfaces both inside and outside the charged object.
Relationship to Coulomb’s Law:
Gauss’s Law and Coulomb’s Law are equivalent. One can be derived from the other. Gauss’s Law is a more general statement, especially useful for complex charge distributions and providing insights into the behavior of electric fields in different media.
Some MCQ about Gauss’s law:
- What does Gauss’s law relate?
A) Magnetic flux to magnetic field
B) Electric flux to the enclosed charge
C) Electric field to the velocity of charges
D) Magnetic field to the velocity of charges
Answer: B) Electric flux to the enclosed charge
2. Gauss’s law is most useful in problems involving:
A) Uniform electric fields
B) Symmetrical charge distributions
C) Asymmetric charge distributions
D) Conductors with no charge
Answer: B) Symmetrical charge distributions
3. Which of the following is the correct interpretation of the flux in Gauss’s law?
A) The total energy stored in the electric field
B) The electric field strength at a given point
C) The amount of electric field passing through a closed surface
D) The potential difference between two points on the surface
Answer: C) The amount of electric field passing through a closed surface
4. The electric flux through a Gaussian surface depends on:
A) The size of the Gaussian surface
B) The shape of the Gaussian surface
C) The amount of charge enclosed by the surface
D) The orientation of the Gaussian surface relative to the field lines
Answer: C) The amount of charge enclosed by the surface
5. For a spherical Gaussian surface surrounding a uniformly charged sphere, what is the electric field inside the sphere?
A) Zero
B) Constant and directed radially outward
C) Proportional to the distance from the center
D) inversely proportional to the square of the distance from the center
Answer: C) Proportional to the distance from the center
6. What is the electric flux through a Gaussian surface when there is no charge enclosed by the surface?
A) Zero
B) Positive
C) Negative
D) Infinite
Answer: A) Zero
7. Which of the following does Gauss’s law fail to explain?
A) The electric field due to a spherical charge distribution
B) The electric field due to an infinite line charge
C) The electric field in conductors at equilibrium
D) The electric field due to a non-symmetrical charge distribution in all cases
Answer: D) The electric field due to a non-symmetrical charge distribution in all cases
8. For a uniformly charged infinite plane, the electric field at a point near the plane is:
A) Zero
B) Constant and perpendicular to the surface of the plane
C) Inversely proportional to the distance from the plane
D) Dependent on the distance squared from the plane
Answer: B) Constant and perpendicular to the surface of the plane